平面的基本性质及应用解析（从几何到现实世界）

电脑常识 2024年10月07日 09:28 20 游客

平面是几何学中的重要概念，也是我们日常生活中不可或缺的元素。本文将从几何学的角度出发，深入探讨平面的基本性质以及它在现实世界中的广泛应用。

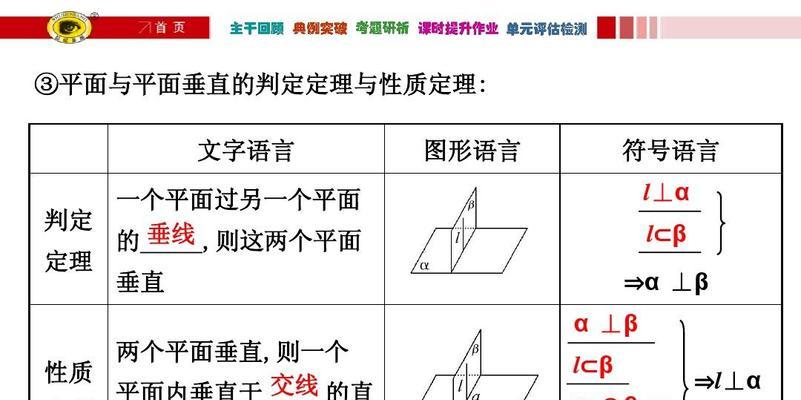
1.平面的定义及特点

平面是指无限延伸的二维空间，其上的任意两点可以通过直线连接。平面具有无限大和无限细的特点，没有起点和终点。

2.平面上的点、线和角

在平面上，我们可以找到无数个点、直线和角。点是平面上最基本的元素，直线可以连接两个点，角则由两条射线共享同一个起始点而成。

3.平行与垂直关系

当两条直线在平面上永远不会相交时，它们被称为平行线。而垂直则表示两条直线或线段之间存在着90度的角度关系。

4.平面的投影

在现实世界中，我们经常使用平面的投影来描述物体。投影是指将三维物体在平面上的影子或映像，通过投影可以看到物体在平面上的形状和大小。

5.平面的对称性

平面具有对称性，即平面上的一部分可以通过某个中心点进行旋转或翻转得到与原图形相同的形状。

6.平面的相交关系

当两个平面相交时，它们会形成一条直线，这条直线称为交线。而两个平面相互垂直时，它们之间的交线称为垂足。

7.平面的平移和旋转

平面可以通过平移和旋转进行变换。平移是指将平面上的所有点沿着固定的方向和距离进行移动，而旋转则是以某一点为中心将平面进行旋转。

8.平面与图形的关系

平面中的图形可以由点、线和角组成。不同的图形有着不同的性质和特点，如三角形、四边形、圆等。

9.平面与立体几何的联系

平面与立体几何密切相关，立体几何中的物体由多个平面组成。平面可以用来描述立体物体的表面特征和几何关系。

10.平面在建筑设计中的应用

在建筑设计中，平面是设计师表达和展示设计意图的重要手段。平面图可以清晰地展示建筑物的布局、尺寸和功能。

11.平面在地理测量中的应用

地理测量中常使用平面坐标系来描述地球上的点、线和面。平面坐标系可以简化测量计算，并方便进行距离和方向的测量。

12.平面在艺术创作中的运用

许多艺术家善于运用平面的特性来表达创作思想，平面艺术作品常通过线条、色彩和形状的组合展现出独特的美感。

13.平面在科学研究中的重要性

在科学研究中，平面被广泛运用于数据分析、图表绘制和模型建立等领域。平面的几何性质为科学家们提供了重要的工具和方法。

14.平面对生活的影响

无论是日常生活中的地图导航，还是电子设备上的平面显示屏，平面都深刻地影响着我们的生活方式和工作方式。

15.平面学习的意义与启示

通过学习平面的基本性质和应用，可以培养我们的空间想象力和几何思维能力，同时也能更好地理解和应用几何学知识。

平面作为几何学中的基本概念，具有丰富的性质和广泛的应用。通过深入了解平面的特点和几何关系，我们可以更好地理解和应用几何学知识，并在现实世界中运用平面的性质解决问题。同时，平面的研究还有助于培养我们的空间想象力和几何思维能力，对我们的学习和生活都具有重要意义。

探索平面的基本性质

平面作为几何学中的一个重要概念，具有许多基本性质，这些性质有助于我们更好地理解和应用平面几何知识。本文将从各个方面介绍平面的基本性质，帮助读者更加深入地认识平面。

平面的定义与特征

平面是由无限多条互相平行而不相交的直线组成的，它没有厚度和边界，可以延展到无穷远处，具有二维的特征。

平面的分类与命名

根据平面上直线的情况，平面可以分为经过两个点或者两条互相垂直的直线的水平平面、垂直平面和倾斜平面，并可以通过这些直线上的点进行命名。

平面上的点、直线与角的关系

在平面上，任意两个点可以确定一条直线，同时一条直线也可以确定两个点。而角是由两条相交的直线所形成，它是衡量两条直线夹角大小的重要工具。

平面上的平行线和垂直线

在平面上，两条直线如果没有交点，即它们不相交，并且方向相同，则称这两条直线是平行的。而垂直线则是指两条直线相交且夹角为90度的情况。

平面上的图形与性质

在平面几何中，有许多常见的图形，如三角形、四边形、圆等。每个图形都有其特定的性质，包括边长、角度、对称性等，通过研究这些性质可以更好地理解和运用平面几何知识。

平面上的相似与全等

在平面上，当两个图形的形状和大小完全相同时，我们称它们是全等的；而当两个图形的形状相同但大小可以不同时，我们称它们是相似的。相似和全等关系是研究平面图形的重要手段。

平面上的对称性

对称是指一幅图形能够在某条中心轴或某个中心点处以一定方式重合自身。对称性在平面几何中起着重要作用，它能够帮助我们分析和解决问题。

平面上的距离和比例

在平面几何中，距离是一个重要的概念，它是用来衡量两点之间的间隔。比例是指两个数或者两个量之间的关系，它能够帮助我们进行度量和推理。

平面上的平移、旋转与翻转

平移是指将一个图形沿着某个方向移动一定的距离，而不改变其形状和大小；旋转是指将一个图形绕着某个点旋转一定的角度，而不改变其形状和大小；翻转是指将一个图形绕着某条直线翻转，使得原先在直线上方的部分移到直线下方。

平面上的投影和相交

在平面几何中，投影是指从一个点向某个方向发出光线，光线与平面相交后形成的图像。相交是指两条直线或者两个图形有公共部分，通过研究它们的相交情况可以得到许多有趣的结论。

平面上的角度和弧度

在平面几何中，角度是衡量两条射线之间的夹角大小的单位，它可以用度数或弧度表示。弧度是角度的另一种计量方式，它更加精确且便于计算。

平面上的投影与平行投影

投影是指从一个空间中的点向某个平面上发出光线，光线与平面相交后形成的图像。平行投影是指在投影过程中，光线与平面平行，投影图像与原物体相似。

平面上的绝对值和方位角

绝对值是指一个数与零的距离，它可以用来表示平面上两点之间的距离。方位角是指从正向x轴到某一射线的逆时针旋转所经过的角度，它可以帮助我们确定平面上某一点的位置。

平面上的中点和分点

在平面几何中，中点是指一个线段上距离两个端点相等的点，它将线段等分为两个相等部分。分点是指在线段上任意给定的一个点，它将线段划分为不同长度的两部分。

平面上的垂足和角平分线

垂足是指从一个点向一条直线引垂线后，垂线与直线交点所在的位置。角平分线是指从一个角的顶点引出一条射线，将该角分为两个相等的角。

通过对平面的基本性质的探索，我们可以更好地理解和运用平面几何知识。平面的定义与特征、分类与命名、点、直线与角的关系、平行线和垂直线、图形与性质、相似与全等、对称性、距离和比例、平移、旋转与翻转、投影和相交、角度和弧度、投影与平行投影、绝对值和方位角、中点和分点、垂足和角平分线等方面的内容，都是我们掌握平面基本性质的重要基础。在学习和应用中不断深入理解这些性质，将有助于我们在解决几何问题时更加熟练和灵活。

标签：讲解

平面的基本性质及应用解析（从几何到现实世界）

探索平面的基本性质

如何解决iPhone信号太差的问题（全面分析原因并提供有效的处理方法）

如何设置苹果自动关机功能（简单操作让您的苹果设备按时关机）

热门文章

最新文章

标签列表

友情链接